- Часть 1. Заряды, потенциалы, напряжение, ток, сопротивление…
- Часть 2. Как работают конденсаторы. Основные параметры конденсаторов.
Итак, конденсатор — это элемент электрической цепи, предназначенный для накопления зарядов. Сразу возникает вопрос: а зачем вообще накапливать заряды? Если вы внимательно читали первую часть, то знаете ответ на этот вопрос: потому что заряды как раз являются источником электрического поля и если в каких-то точках соотношения положительных и отрицательных зарядов разные, то между этими точками будет существовать разность потенциалов. То есть заряженный конденсатор (когда он накопил некоторый заряд) — это как бы мини источник ЭДС, который может отдавать накопленные заряды, поддерживая в цепи электрический ток (при этом сам он, естественно, будет разряжаться). Его принципиальное отличие от источника ЭДС (в котором сторонние силы, обусловленные химической реакцией, переменным магнитным полем или ещё чем-то, разделяют заряды и поддерживают разность потенциалов на его выводах) в том, что в конденсаторе нет сторонних сил (т.е. он сам внутри себя заряды не разделяет) и разность потенциалов между его выводами обеспечивается только теми зарядами, которые он накопил в процессе зарядки (то есть теми зарядами, которые пришли к нему извне).
И ещё одно. Что значит "накапливает заряд"? На самом деле выражение "накапливает" в данном случае означает перераспределение зарядов между обкладками конденсатора и внешней цепью. То есть если заряды на обкладках перераспределятся таким образом, что суммарный заряд на положительной обкладке будет на величину Q больше, чем на отрицательной, то говорят, что конденсатор накопил заряд Q. Куда заряды будут втекать и откуда утекать зависит от того, какая в начальный момент была разность потенциалов между соответствующим выводом конденсатора и той точкой внешней цепи, к которой этот вывод подключили. Короче говоря, главное, что в результате вот этого "накопления" разность зарядов между положительной и отрицательной обкладками станет равна Q.
Важнейшие характеристики конденсатора — это ёмкость и номинальное напряжение.
Итак, сначала ёмкость. Ёмкость — это параметр, который устанавливает связь между изменением заряда на обкладках и изменением напряжения между выводами конденсатора. Ёмкость показывает насколько сильно будет изменяться заряд на обкладках конденсатора при изменении напряжения между его выводами. Ну и, соответственно, от неё же зависит насколько сильно будет изменяться напряжение между выводами при изменении заряда на обкладках. Математически эта связь описывается такой формулой: C=dQ/dU, где dQ — изменение заряда, dU — изменение напряжения между выводами конденсатора. То есть численное значение ёмкости (то, что написано на вашем кондёре) показывает: на сколько Кулон нужно изменить заряд конденсатора, чтобы напряжение между его выводами изменилось на 1 В.
Чтобы было понятнее, можно привести такую аналогию:
Будем считать, что давление воздуха аналогично потенциалу, а количество воздуха (не важно, количество вещества или масса) аналогично заряду. Вполне законное сравнение, если учесть, что давление воздуха в каком-то замкнутом пространстве стремится выровняться по всему объёму и при этом воздух перемещается из областей с высоким давлением в области с низким давлением, причём чем больше разность давлений, тем, при прочих равных условиях, он это делает быстрее (помните, чем больше разность потенциалов — тем больше сила тока, при одинаковом сопротивлении?).
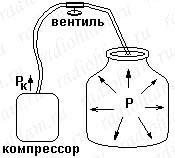
Далее, представьте, что у нас есть закрытая крышкой банка (это будет аналог конденсатора), в которую через дырку в крышке вставлена трубка. Если давление снаружи и внутри банки равно атмосферному, то разности давлений нет, то есть напряжение равно нулю и воздух не будет выходить из банки наружу и не будет заходить снаружи в банку. Теперь представьте, что мы подключили трубку к компрессору, который создаёт на выходе некоторое избыточное давление Pк (избыточное, — то есть на величину Pк больше атмосферного). Компрессор в данном случае будет аналогичен источнику ЭДС. При этом все я думаю прекрасно понимают, что если открыть вентиль, то воздух по трубке начнёт закачиваться в банку, то есть количество воздуха в банке начнёт увеличиваться. Или можно сказать, что наш конденсатор начнёт заряжаться (банка же у нас — это конденсатор). Но по мере увеличения в банке количества воздуха — у нас будет расти и давление в банке, соответственно будет расти разность между давлением в банке и атмосферным давлением (в нашем примере эта разность — аналог напряжения). Давление в банке будет расти до тех пор, пока не сравняется с давлением, создаваемым компрессором. После того, как это произойдёт — ток воздуха по трубке прекратится.
Так вот, величиной, аналогичной электрической ёмкости, в данном случае будет не объём банки (первая ассоциация с ёмкостью, которая приходит на ум, да?), а величина, показывающая на сколько нужно изменить массу воздуха в банке, чтобы давление в ней изменилось на 1 Паскаль. То есть ёмкость в данном случае будет связывать изменение количества воздуха в банке (изменение массы, а не объёма, он у нас постоянный, банка стеклянная и не растягивается) с изменением давления в ней. Математически это выглядело бы вот так C=dM/dP.
Надеюсь с ёмкостью всё понятно, поэтому перейдём ко второй важнейшей характеристике конденсатора — номинальному напряжению. Тут вообще всё просто. Рассмотрим опять аналогию с банкой. Понятно, что если накачивать и накачивать в неё воздух, то давление в ней будет расти, расти и в конце концов банка не выдержит и лопнет. То есть при превышении определённой разницы давлений внутри и снаружи (или можно сказать при превышении напряжения) нашу банку-конденсатор просто разорвёт на части. Точно также обстоят дела и с электрическим конденсатором. Если зарядить его выше некоторого напряжения, то произойдёт пробой, конденсатор разрушится и перестанет функционировать. Обычно в маркировке для конденсатора указывают номинальное напряжение — такое, при котором он может в течение всего срока службы эксплуатироваться без опасений, что произойдёт пробой, разрушение или ещё какие-то его повреждения. В принципе, конденсаторы могут выдерживать некоторые перенапряжения (величина зависит от типа конденсатора, материала диэлектрика и т.д), но тем не менее заряжать конденсатор до напряжения выше номинального крайне не рекомендуется, потому что в этом случае производитель уже не даст гарантии, что параметры конденсатора не ухудшатся и он не разрушится.
Давайте рассуждать дальше. Итак, мы знаем, что напряжение между выводами конденсатора увеличивается вследствие перераспределения зарядов между обкладками и внешней цепью и напрямую связано с количеством накопленного конденсатором заряда. Но заряды у нас не перемещаются мгновенно, следовательно, для того, чтобы конденсатор зарядился и напряжение между его выводами выросло — требуется некоторое время. Точно так же и давление воздуха в банке не вырастает мгновенно при подключении к ней компрессора, а постепенно растёт по мере увеличения количества закачанного воздуха. От чего же зависит скорость заряда конденсатора? Очевидно, что она зависит от того, насколько быстро перераспределяются заряды (то есть от силы тока).
Теперь давайте эти логические рассуждения подкрепим математикой. Возьмём формулу, связывающую ёмкость, заряд и напряжение и перепишем её в таком виде: dQ=C*dU, а затем обе части продифференцируем по времени, получится: dQ/dt=C*dU/dt. В левой части я думаю все узнали выражение для силы тока, поэтому заменив dQ/dt на I, окончательно получим: I=C*dU/dt — выражение, связывающее ёмкость и мгновенные значения силы тока и напряжения на конденсаторе.
"Ну и зачем нам эта формула?", — спросят некоторые товарищи, и будут очень сильно неправы, потому что это вообще-то основная формула, которая используется в расчётах цепей с конденсаторами.
Что нам ещё интересно? Интересно, например, сколько энергии накоплено в конденсаторе и где эта энергия сосредоточена. Как это узнать? Всё так же просто, как и с источником ЭДС, о котором мы говорили в первой части. Раз на обкладках накапливаются заряды и обкладки разделены диэлектриком, значит между обкладками существует электрическое поле. В этом-то электрическом поле и сосредоточена энергия конденсатора. Как её оценить? Очевидно так же, по величине работы, которую это поле может совершить по перемещению зарядов.
Представим, что у нас есть полностью заряженный конденсатор (при этом напряжение на его выводах равно U1) и мы замкнули его выводы между собой (не важно через какое сопротивление). Какая мгновенная мощность будет при этом выделяться в нашей цепи? Как мы знаем мгновенная мощность определяется выражением P=U*dQ/dt. Работа за какой-то промежуток времени — это определённый интеграл от мгновенной мощности на этом промежутке времени. Очевидно, что для того, чтобы посчитать всю запасённую конденсатором энергию, надо измерять работу за промежуток времени от момента, когда мы замкнули полностью заряженный конденсатор до момента его полного разряда, то есть от момента, когда напряжение на конденсаторе было равно U1 до момента, когда напряжение на нём станет равным нулю. Это мы запомним. Изменение напряжения и изменение заряда связаны соотношением dU=dQ/C, отсюда dQ=dU*C. Подставив это выражение в формулу для мощности, получим: P=C*U*dU/dt. Перенесём dt в левую часть и проинтегрируем. В левой части получим работу, а в правой определённый интеграл от напряжения. Какие пределы напряжения брать для вычисления этого определённого интеграла? А вот теперь вспоминайте то, что чуть выше запомнили: "от момента, когда напряжение на конденсаторе было равно U1 до момента, когда напряжение на нём станет равным нулю". Значит в правой части интеграл надо брать от U1 до нуля. В итоге получится A=C*U12/2. Эта работа как раз и равна энергии, запасённой конденсатором. Ровно столько энергии он забирает из внешней цепи, когда заряжается, и ровно столько же энергии отдаёт во внешнюю цепь при разряде.
Ладно, с основными параметрами мы разобрались, где сосредоточена энергия и какова её величина — нашли, теперь переходим к неосновным параметрам, которые характеризуют различные потери на конденсаторе и при определённых условиях бывают очень важны, но значения которых бывает не так просто отыскать.
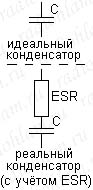
Первый такой важный параметр — это эквивалентное последовательное сопротивление (обычно употребляют английскую аббревиатуру от equivalent serial resistance — ESR). Что это вообще такое? Дело в том, что при движении по обкладкам и по металлическим выводам конденсаторов электроны испытывают точно такое же сопротивление, как и при движении по любому другому проводнику. Поэтому если мы хотим учесть ESR, то наш конденсатор следует рассматривать как элемент, который обладает не только ёмкостью (обычно именно так представляют идеальный конденсатор), но и последовательно соединённым с ней сопротивлением. Куда девается энергия, отнимаемая у упорядоченно движущихся зарядов в результате наличия сопротивления? Она точно так же, как и в обычном резисторе идёт на нагрев, только в данном случае нагреваются выводы и обкладки конденсатора. Итак, первое, почему важно учитывать ESR — потому, что это основной параметр, определяющий потери энергии в конденсаторе (следовательно от него зависит нагрев конденсатора, если токи заряда/разряда достаточно большие, то нагрев может быть значительным), кроме того, ESR влияет на сглаживающие способности конденсатора.
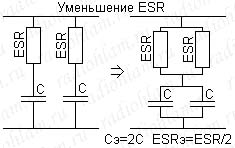
Именно из-за увеличения ESR при старении обычно вздуваются конденсаторы в блоках питания (ну и ещё из-за уменьшения сопротивления изоляции, но об этом ниже). Можно ли как-то уменьшить это негативное влияние ESR? Да легко, для этого надо подключить параллельно несколько конденсаторов, при этом сопротивления тоже окажутся включенными параллельно. В мощных блоках питания так и делают — ставят целые ряды параллельно включенных конденсаторов, хотя в принципе их можно было бы заменить всего одним или двумя, но большей ёмкости. На рисунке показано как уменьшается ESR при параллельном подключении двух одинаковых конденсаторов. Так что, как видите, включить два конденсатора по 470 мкФ может быть более выгодно, чем один на 1000 мкФ.
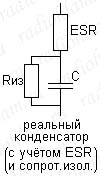
Второй важный параметр — это сопротивление изоляции. Этот параметр важен потому, что он позволяет оценить так называемые токи утечки. Что это такое? В принципе у нас обкладки конденсатора разделены диэлектриком, который не пропускает электрический ток, но это в идеале. Реально же сопротивление изоляции не бесконечно велико и, соответственно, когда между обкладками конденсатора есть напряжение, то через изоляцию текут так называемые токи утечки (пусть и очень очень маленькие). С учётом сопротивления изоляции конденсатор можно представить как ёмкость, шунтированную резистором. Каков эффект протекания этих токов? Они естественно тоже влияют на нагрев и сглаживающие свойства конденсатора. Обычно сопротивление изоляции всё таки огромно и токи утечки настолько мизерные, что их вообще не учитывают, но по мере старения конденсатора сопротивление изоляции может ослабнуть и токи утечки могут многократно возрасти. Иногда даже можно услышать: "появились токи утечки", как бы подчёркивая, что раньше они были настолько малы, что их вообще не брали в расчёт. Токи утечки, в свою очередь тоже ведут к повышенному нагреву конденсатора. В этом случае конденсатор просто выкидывают и ставят новый.
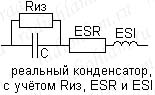
Ещё одним важным параметром является эквивалентная последовательная индуктивность — ESI. Она так же как и ESR обусловлена собственной индуктивностью выводов и обкладок конденсатора. Этот параметр начинает оказывать заметное влияние с ростом частоты. Помните, реактивное сопротивление ёмкости с ростом частоты уменьшается, а индуктивности, наоборот, увеличивается. Соответственно, при определённой частоте паразитная индуктивность может начать оказывать большее влияние, чем собственно, ёмкость. Именно поэтому, например, большие толстые электролиты, имеющие большую ESI, крайне плохо справляются с фильтрацией высокочастотных помех, а мелкая керамика, у которой ESI маленькая, — отлично. Хотя по логике, чем больше ёмкость — тем меньше реактивное сопротивление на одной и той же частоте, но в том-то и дело, что на высоких частотах главную роль играет уже не ёмкость, а паразитная индуктивность и ESR. Эквивалентная схема реального конденсатора с учётом ESI приведена на рисунке. Из этой схемы вытекает ещё одно интересное наблюдение. Если мы для борьбы с ESR включили несколько конденсаторов параллельно, то ESR мы конечно уменьшим, но при этом ESI такой сборки — увеличится. Это тоже может быть важным. Ну и хотелось бы добавить, что на нормальных платах ряды электролитов обычно шунтированы такими же рядами керамики (имеющей низкие ESI и ESR), как раз для фильтрации ВЧ помех, которые остаются незамеченными электролитами (с их высокими ESI и ESR).
Идём дальше. Ещё один такой параметр, который очень трудно найти, но тем не менее он существует и иногда его надо учитывать — это максимально допустимый пульсирующий ток через конденсатор, или сокращённо RCR (ripple current ratio, что можно перевести как "величина пульсирующего тока" или "размер токовых пульсаций").
Ну и наконец последнее, на чём хочется остановиться — это тангенс угла потерь (tgd). Этот параметр равен отношению активной мощности, выделяемой на конденсаторе к реактивной мощности. Активная мощность — это понятное дело в основном мощность обусловленная ESR и сопротивлением изоляции. Реактивная мощность обусловлена ёмкостью и паразитной индуктивностью. Я думаю вполне понятно, что tgd также очень сильно зависит от частоты (потому что компоненты, которые определяют этот параметр зависят от частоты), поэтому сравнивать tgd у разных конденсаторов имеет смысл только когда они измерены для одной и той же частоты. Обычно есть стандартные частоты, на которых измеряют tgd. Буржуины иногда выражают этот параметр в % и называют DF (dissipation factor — фактор рассеяния или фактор потерь) или просто D. А поскольку они очень дотошные товарищи, то у них иногда можно найти даже график зависимости DF от частоты (один раз такой видел).
Обычно если у производителей конденсаторов и можно что-то найти, то это ESR или tgd (DF), но тем не менее надо помнить и про паразитную индуктивность, и про возможность появления токов утечки, и про максимальный ток.
Cпособы маркировки конденсаторов.
- Часть 1. Заряды, потенциалы, напряжение, ток, сопротивление…
- Часть 2. Как работают конденсаторы. Основные параметры конденсаторов.