Теория работы и расчёт неизолированного понижающего преобразователя. Часть 2. Анализ различных режимов работы и расчёт элементов buck-конвертера

1. Часть 1. Введение. Теоретические основы buck-конвертера
2. Часть 2. Анализ различных режимов работы и расчёт элементов buck-конвертера
3. Часть 3. Переходим от идеальных элементов к реальным.

Прежде чем приступать к анализу — давайте вспомним несколько картинок и формул из первой части, а именно: схему buck-конвертера (без схемы управления), графики напряжений и токов в точке А, а также формулы, описывающие эти токи и напряжения в зависимости от состояния ключа.

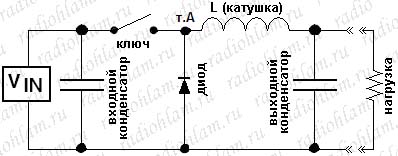
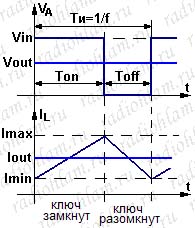
— при замкнутом ключе напряжение в т.А равно V_in, ток в катушку и далее течёт через ключ от источника питания и описывается формулой I=(V_in-V_out)*t/L;

— при разомкнутом ключе напряжение в т.А равно нулю, ток в катушку и далее течёт через диод и описывается формулой I=-V_out*t/L.

Кроме того, давайте вспомним, что среднее за период падение напряжения на катушке индуктивности равно нулю (и, соответственно, среднее за период напряжение в т.А равно V_out), а так же то, что средний за период ток через катушку (ну и, разумеется, через т.А тоже), равен выходному току (I_out).

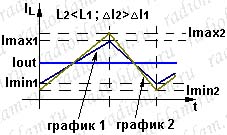
Теперь давайте подумаем — как изменятся наши графики, если мы увеличим входное напряжение, но при этом выходное напряжение, ток нагрузки и период импульсов останутся прежними.

Сначала рассмотрим график напряжения в т.А. Единственный вариант сделать так, чтобы среднее за период напряжение не изменилось (оно у нас как вы помните равно выходному), — это изменить скважность импульсов, — сократить время открытого состояния ключа (t_on) и увеличить время закрытого состояния (t_off). Только в этом случае при увеличении V_in среднее значение, равное (V_in*t_on+0*t_off)/(t_on+t_off) не изменится.

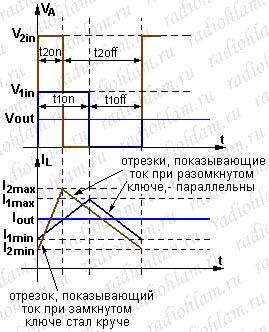
Хорошо, с этим разобрались, момент переключения на нашем графике сдвинулся влево, но как теперь провести новые линии на графике тока? Давайте опять подумаем и внимательно посмотрим на формулу, описывающую график тока через катушку в то время, когда ключ разомкнут: I=-V_out*t/L. Как видите, в этой формуле от того, что мы изменили входное напряжение, абсолютно ничего не изменилось. Изменится у нас только время, в течении которого ток описывается этой формулой), а коэффициент угла наклона этой прямой, определяемый выражением -V_out/L, останется прежним. То есть новый отрезок графика, соответствующий состоянию когда ключ разомкнут, должен проходить параллельно старому отрезку. Что ещё мы знаем? Ещё мы знаем, что поскольку выходной ток не меняется, то прямая I(t)=I_out проходит через середины наших отрезков, показывающих как тёк ток при различных состояниях ключа (в первой части мы разбирались — почему так; это для выполнения закона сохранения заряда). Вот в общем-то и всё, — проводим новый отрезок параллельно старому, таким образом, чтобы прямая I(t)=I_out проходила через его середину. Концы нашего нового отрезка показывают новые значения минимального и максимального токов через катушку. Теперь осталось только соединить их линией на том промежутке, где ключ замкнут и наш график построен.

Что мы в итоге видим? Видим, что с увеличением входного напряжения увеличилась скважность и увеличился размах пульсаций тока (у нас I_2max > I_1max, а I_2min < I_1min). Ещё мы видим, что участок графика, показывающий как изменялся ток при замкнутом состоянии ключа стал круче, это в общем-то и логично. Коэффициент угла наклона этого участка определяется как мы помним формулой k=(V_in-V_out)/L, так что при увеличении V_in этот коэффициент стал больше, соответственно, этот участок графика стал круче.

Аналогичным образом можно показать, что при уменьшении входного напряжения, если при этом не меняются выходное напряжение и ток, — скважность и размах пульсаций тока будут уменьшаться. То есть при неизменном выходном токе максимальные пульсации тока мы получим при максимальном входном напряжении, а максимальное время открытого состояния (минимальную скважность) — при минимальном входном напряжении.

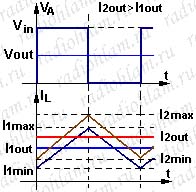
Теперь давайте подумаем, что будет происходить, если уменьшать или увеличивать выходной ток при неизменном входном и выходном напряжении.

Тут на самом деле всё очевидно. Скважность у нас не изменится — поскольку в формуле V_out=V_in*t_on+0*t_off)/(t_on+t_off) ничего не изменилось, а график тока просто будет целиком смещаться вверх (при увеличении выходного тока) или вниз (при уменьшении выходного тока). Соответственно, максимальный пиковый ток мы получим при максимальном выходном токе, а минимальный — при минимальном выходном токе (размах пульсаций тока при этом не меняется).

Исходя из всего вышесказанного можно уже сделать некоторые выводы. Например, такой, что максимальные пульсации тока мы получим при максимальном входном напряжении и максимальном выходном токе. Или такой, что максимальное время открытого состояния ключа будет при минимальном входном напряжении.

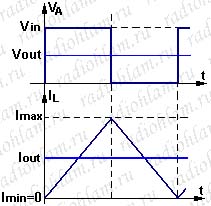
Теперь представьте, что мы уменьшали, уменьшали выходной ток (при этом наш график сдвигался, сдвигался вниз) и доуменьшали его до такой степени, что график тока через катушку у нас упёрся в ось t, то есть минимальный ток, Imin, стал равен нулю. Вместо этого можно было бы увеличивать и увеличивать входное напряжение, при этом как вы помните размах пульсаций тока увеличивается и минимальное значение тока, Imin, так же уменьшается, но мы будем рассматривать именно вариант с уменьшением выходного тока, поскольку в случае с увеличением входного напряжения картинка будет меняться несколько сложнее (придётся ещё скважность менять), хотя смысл тот же и формулы мы в итоге получим те же. Итак, смотрите график слева. Что означает такая картинка? Она означает, что за время закрытого состояния ключа катушка индуктивности расходует всю запасённую в ней энергию.

/Тут, для лучшего осознания, сделаем небольшое лирическое отступление, поскольку может возникнуть вопрос: «Мы же вроде говорили, что катушка в установившемся режиме каждый цикл сколько запасает — столько потом и отдаёт и не важно спадает ток до нуля или нет?» Всё правильно, но тут нет никакого противоречия. Если катушка сколько запасает — столько и отдаёт, то это вовсе не означает, что в ней больше ничего не остаётся. Вспомните школьный курс физики: запасённая в катушке энергия равна L*I²/2. Так что если в момент переключения ключа ток в катушке индуктивности не равен нулю — значит в катушке ещё остаётся запас энергии и если бы этого переключение не произошло, то катушка могла бы ещё некоторое время поддерживать в цепи ток. А вот когда ток через катушку спадает до нуля — это как раз означает, что энергии у катушки больше нет совсем, вообще нисколько. То есть когда наш график не касается оси t и целиком расположен выше неё, то в катушке постоянно есть некоторый запас энергии. Да, в установившемся режиме он увеличивается при нарастании тока через катушку, ровно настолько же, насколько потом уменьшается при уменьшении тока, но он никогда не уменьшается до нуля./

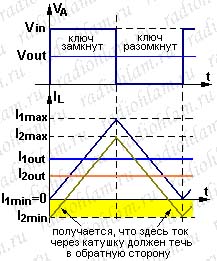
Ну ладно, вернёмся опять к нашей ситуации. Мы значит ток уменьшали, уменьшали и в итоге наш график тока через катушку упёрся в ось t. Что будет если продолжать уменьшать ток? Давайте попробуем как раньше — просто сдвинуть график тока вниз. У нас получилось, что часть графика теперь расположена ниже оси t, то есть ток там отрицательный, то есть должен течь в обратную сторону! Такого естественно произойти не может, поскольку через диод ток в обратную сторону не течёт.

Что же будет происходить в реальности? В реальности всё будет очень просто — ток через катушку уменьшится до нуля и так и будет ноль, пока ключ снова не откроется и ток через катушку не начнёт снова увеличиваться. Каким при этом должно быть напряжение на катоде диода? Ну тут вообще просто. Ключ — разомкнут, диод закрыт, катушка подключена только к выходному конденсатору и тока через неё нет — значит падение напряжения на катушке равно нулю, то есть напряжение на катоде диода равно выходному напряжению.

Такой режим работы преобразователя, когда ток в катушке некоторое время равен нулю, — называется "прерывистым" (по буржуински — discontinuos mode). В противоположность ему, режим, при котором ток у нас никогда не становился равным нулю (то, что мы рассматривали ранее, когда график тока у нас целиком лежал выше оси t и нигде её не касался), называется "непрерывным" (по буржуински — continuos mode). Соответственно, ситуация, когда наш график тока касается нижними вершинами оси t — это пограничное состояние между "прерывистым" и "непрерывным" режимами, оно иногда называется "критический" режим.

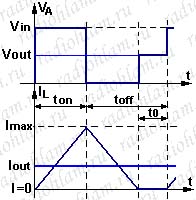
Давайте нормально нарисуем графики для "прерывистого" режима и подумаем, — что при этом будет таким же, как и при "непрерывном" режиме, а что будет отличаться.

Во-первых, мы видим, что отличается график напряжения, — на переднем фронте этого графика у нас появилась ступенька, равная выходному напряжению.

Далее, — на тех участках, где ток растёт и уменьшается — расти и уменьшатся он будет точно по таким же как и раньше законам: I(t)=(V_in-V_out)*t/L для участка роста, и I(t)=-V_out*t/L для участка уменьшения.

Что изменится? Очевидно, что изменятся наши уравнения, связывавшие время замкнутого и разомкнутого состояния ключа с входным и выходным напряжениями, а так же уравнение, связывавшее максимальный, минимальный и выходной токи.

Для того, чтобы написать уравнения для "прерывистого" режима обозначим через t₀ время, в течении которого ток через катушку был равен нулю. Ну вот, теперь давайте составлять уравнения.

Поскольку законы физики за то время, пока мы всё это понаписали, не изменились, то среднее за период напряжение на катушке у нас по прежнему равно 0 (в первой части мы разбирались почему), среднее напряжение на катоде диода равно V_out. Отсюда мы имеем:

V_out*(t_on+t_off)=V_in*t_on+0*(t_off-t₀)+V_out*t₀, после преобразования получаем:

V_out*(t_on+t_off-t₀)=V_in*t_on

И второе, средний ток через катушку по-прежнему равен выходному току. Отсюда получаем:

I_out*(t_on+t_off)=0,5*I_max*t_on+0,5*I_max*(t_off-t₀)+0*t₀, после преобразования:

I_out*(t_on+t_off)=0,5*I_max*(t_on+t_off-t₀)

Для полноты картины осталось добавить ещё одно уравнение: t_on+t_off=t_и, где t_и=1/f — период импульсов. Ну вот, теперь решив эту систему уравнений совместно с двумя уравнениями, описывавшими как изменяется ток на участках роста и уменьшения, можно получить весь расклад по работе нашего преобразователя в "прерывистом" режиме.

Какие мы ещё выводы можем сделать, узнав о существовании этого самого "прерывистого" режима? Ну главный вывод состоит в том, что поскольку в этот режим мы попали при увеличении входного напряжения и уменьшении выходного тока, то получается, что для любого buck-конвертера, у которого минимальный ток нагрузки равен нулю существует область с таким соотношением входного напряжения и выходного тока, когда наш конвертер работает в "прерывистом" режиме. То есть любой buck-конвертер работает в обоих режимах, смотря какое взять входное напряжение и выходной ток.

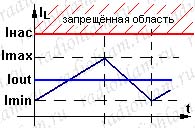
Теперь давайте подумаем, а чем собственно наш график тока ограничен сверху, и ограничен ли вообще? Давайте вспомним, что наш график тока — это не просто график тока, а график тока через катушку индуктивности, а у каждой катушки индуктивности есть такой параметр, как ток насыщения. Насыщение — это, как вы наверное помните, такая нехорошая штука, когда катушка больше не может запасать энергию в магнитном поле так же хорошо как раньше, индуктивность её падает практически до нуля, у неё остаётся почти что только активное сопротивление (почему «практически» и «почти что», а так же что и как вообще происходит в катушках индуктивности мы отдельно поговорим), как следствие в ней начинает очень быстро нарастать ток, ну и короче ни к чему хорошему это не приводит (минимум — просто к нестабильной работе преобразователя, максимум — к выгоранию силового ключа). Поэтому логично, что если мы хотим, чтобы наш преобразователь нормально работал, то наш ток никогда не должен становиться выше тока насыщения катушки индуктивности (на рисунке слева Iнас — ток насыщения, «запрещённая область» — область, в которую наш график никогда не должен заходить). Это нам пригодится когда будем катушку индуктивности выбирать.

Далее, как мы ранее уже разбирались, — от величины индуктивности зависят коэффициенты углов наклона участков роста и уменьшения тока на графике тока через катушку индуктивности. Причём, чем больше L — тем более пологими будут эти участки, то есть меньше будут пульсации тока (I_max-I_min). Почему же мы тогда не мотаем максимально возможные индуктивности на наших катушках, ведь чем меньше пульсации тока — тем легче их сглаживать? Так вот, это происходит потому, что коэффициенты углов наклона наших участков роста и уменьшения тока через катушку индуктивности, а следовательно и величина индуктивности, и размах пульсаций тока — определяют скорость работы нашего преобазователя. То есть, если мы изменили, например, выходной ток, то от описанных выше параметров зависит скорость переходного процесса, в результате которого на выходе нашего преобразователя снова установится требуемое стабильное напряжение. Причём чем более пологий у нас график тока — тем медленнее протекает переходный процесс, а чем график тока круче — тем переходный процесс протекает быстрее. Поэтому при слишком большой индуктивности наш преобразователь получится слишком медленным.

Ну и вот как-то так принято, что для нормальной работы преобразователя (чтоб и скорость была нормальной и пульсации приемлемыми), при расчётах берут максимальные пульсации тока (размах от I_min до I_max) равными 30-40% от максимального выходного тока (I_{out max}). Для относительных пульсаций тока даже обозначение своё придумали — LIR=(I_max-I_min)/I_out. Понятно, что эти самые пульсации (и по абсолютной величине и относительные) будут разные при разном выходном токе и разном входном напряжении (например на границе между "непрерывным" и "прерывистым" режимом LIR=200%), но нас интересуют самые большие по абсолютной величине пульсации. А когда там у нас самые большие пульсации-то? При максимальном входном напряжении и максимальном выходном токе. Понятно, что, если при этом мы хотим получить LIR=30%, то преобразователь у нас должен работать в «непрерывном» режиме (при расчётах будем использовать формулы для этого режима). Соответственно, индуктивность рассчитывается исходя из максимальной абсолютной величины пульсаций тока именно для самого худшего случая.

Теперь давайте всё вышесказанное подытожим и исходя из этого приведём некий общий алгоритм расчёта:

Итак, какие данные мы имеем для расчёта? Пусть мы хотим рассчитать такой преобразователь, чтобы максимальный выходной ток у него был I_{out max}, диапазон входного напряжения от V_{in min} до V_{in max}, выходное напряжение V_out и работать он у нас будет на частоте f. Кроме того мы хотим, чтобы величина пульсаций тока по абсолютной величине не превышала LIR*I_{out max}. Из этих данных составляем уравнения:

t_on+t_off=1/f

(V_{in max}-V_out)*t_on/L=LIR*I_{out max}

V_out*t_off/L=LIR*I_{out max}

Решив эту систему уравнений мы получим, что индуктивность у нас должна быть равна:

L=(1-V_out/V_{in max})*V_out/(LIR*I_{out max}*f)

Максимальный пиковый ток: I_{pk max}=(1+LIR/2)*I_{out max}. Соответственно, катушка должна быть выбрана так, чтобы её ток насыщения был больше I_{pk max} (то есть габариты и материал середчника должны быть такими, чтобы, намотав на этом сердечнике требуемую индуктивность, ток насыщения катушки был больше максимального пикового тока).

Минимальная ёмкость выходного конденсатора (мы её в первой части рассчитывали):

С_min=(LIR/2)*I_{out max}/(4*V_p-p*f)

Вот тут, кстати, стоит добавить, что эта формула для конденсатора была у нас получена для самой плохой ситуации в установившемся режиме (при максимальных пульсациях тока), но реально самая плохая ситуация (самый большой всплеск напряжения) будет при резком падении тока нагрузки от максимума до нуля в тот момент, когда ток через катушку максимален. Это правда будет разовый такой всплеск, в отличии от постоянных пульсаций в установившемся режиме, но если его не учитывать, то можно и пальнуть что-нибудь при резком изменении нагрузки. В следующей части допишу про эту ситуацию и как кондёр посчитать, чтоб этот всплеск был не больше определённой величины, а сейчас хорош, чё-то я уже утомился.

Кроме того, в следующей части я напишу, как такой преобразователь будет работать не с идеальными, а с реальными элементами, как при этом изменятся наши графики и расчёты.

1. Часть 1. Введение. Теоретические основы buck-конвертера
2. Часть 2. Анализ различных режимов работы и расчёт элементов buck-конвертера
3. Часть 3. Переходим от идеальных элементов к реальным.