Если полоса пропускания (Δf=fв-fн) широка и сравнима со средней геометрической частотой fср2=fв*fн, или если fв/fн>2, то полосовой фильтр может быть составлен из последовательно соединенных ФНЧ и ФВЧ, у которых имеется перекрывающийся участок характеристики K(ω). При этом необходимо разделять ФНЧ и ФВЧ повторителем, чтобы избежать взаимного влияния.
Если же fв/fн→1, то применяют специальные полосовые фильтры.
Простейший пассивный полосовой фильтр — это мост Вина.

Запишем уравнения для Uвых и Uвх (в операторной форме):
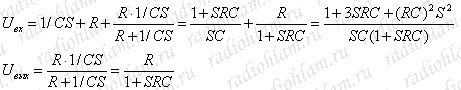
Отсюда, разделив второе уравнение на первое, получим операторное выражение для коэффициента усиления (для удобства произведем замену τ=RC):
![]()
Произведем замену S=jω, — получим зависимость K(jω):
![]()
Выделим в этом выражении вещественную и мнимую части:
![]()
Теперь можно получить выражения для построения АЧХ и ФЧХ:
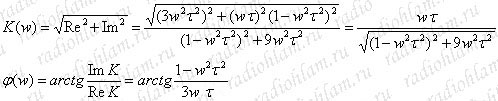
Коэффициент усиления данного фильтра при ω→0 и при ω→∞ равен нулю, при этом:
- tg(φ)→∞ φ→π/2 при ω→0
- tg(φ)→-∞ φ→-π/2 при ω→∞
Особенность моста Вина (которая позволяет использовать его как полосовой фильтр) в том, что на определенной частоте ωр (которая называется частотой квазирезонанса) АЧХ моста имеет максимум.
Найдем ωр из условия, что в точке максимума производная обращается в ноль:
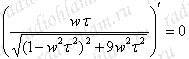
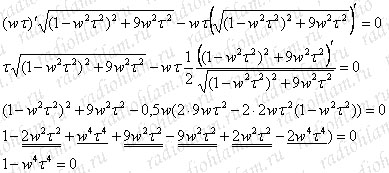
Отсюда находим ωр = 1/τ = 1/RC, подставив ωр в K(ω) найдем: K(ωр)=1/3
Найдем частоты, на которых Kmax уменьшается в √2 раз:
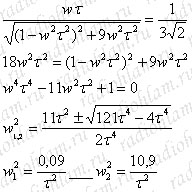
Отсюда находим ωн и ωв (нижнюю и верхнюю частоту среза):
ωн = 0,3/τ = 0,3/RC
ωв = 3,3/τ = 3,3/RC
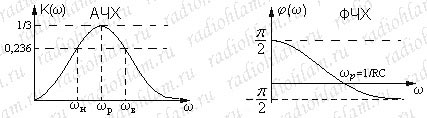
Мне показалось, что в выражении для построения ФЧХ ошибка. Вместо «arctg((1-w^2*t^2)/(3*w^2*t^2))», надо написать «arctg((1-w^2*t^2)/(3*w*t))». То есть, в знаменателе квадраты у омеги и тау убрать.
Хм, точно. Так и есть. Поправил формулу и график ФЧХ.