Представленная и описанная в этой статье схема позволяет изготовить малогабаритный блок питания для низкоточных схем, преобразующий переменное сетевое напряжение в постоянное напряжение заданного уровня.
Принцип действия схемы очень простой — последовательно с выпрямительным мостом (с которого снимается рабочее напряжение на сглаживающий конденсатор и нагрузку) включен конденсатор, на котором гасится избыточное напряжение. Собственно, из-за этого гасящего конденсатора схема и получила своё название. Другое название этого конденсатора — балластный, соответственно, другое название схемы — схема с балластным конденсатором.
Базовый вариант схемы выглядит следующим образом:
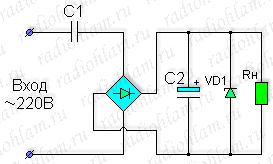
Добавлю некоторые пояснения касательно предложенной схемы. Почему в качестве балласта используется именно конденсатор, а не резистор? Потому что резистор, при протекании через него электрического тока, очень сильно нагревается, в то время как конденсатор не греется совсем (за исключением небольшого нагрева, обусловленного омическим сопротивлением обкладок и выводов). Почему же тогда всегда вместо резисторов конденсаторами для гашения «лишнего» напряжения не пользуются? Потому что через конденсатор может протекать только переменный ток, а постоянный — никак.
Так же, как и рассмотренный ранее блок питания с конденсаторным делителем, блок питания с гасящим конденсатором относится к бестрансформаторным и не имеет гальванической развязки с сетью 220В, то есть прикосновение к любой его части запрещено и может вызвать поражение электрическим током. Тем не менее, существует масса вариантов, для которых применение такого блока питания вполне оправдано, например, в малогабаритных корпусированных приборах с микроконтроллерным управлением, когда случайное прикосновение к токоведущим частям исключено, большой ток не нужен, а размер критически важен.
Логическое обоснование расчётов и математический вывод формул, позволяющих связать ток нагрузки с ёмкостью гасящего конденсатора, я убрал под спойлер, чтобы не травмировать психику тех, кто не особо силён в физике и математике, а также чтобы не перегружать лишней информацией тех, кому это просто не интересно.
Итак, процессы в этой схеме будут достаточно нелинейны, поэтому при рассчётах придётся делать различные упрощения и допущения.
Для начала давайте будем считать, что ёмкость конденсатора C2 достаточна для полного сглаживания пульсаций напряжения после моста, то есть напряжение на конденсаторе C2 = const. Далее попробуем нарисовать пару графиков, — напряжение на входе моста (UM) и ток через конденсатор C1 (IC1), опираясь на график сетевого напряжения UС(t). Будем считать, что сетевое напряжение у нас изменяется по синусоидальному закону и имеет амплитуду Uca (вообще-то рисовать мы будем косинусоиду, нам так будет удобнее, но это по сути одно и то же, только косинусоида сдвинута относительно синусоиды на π/2).
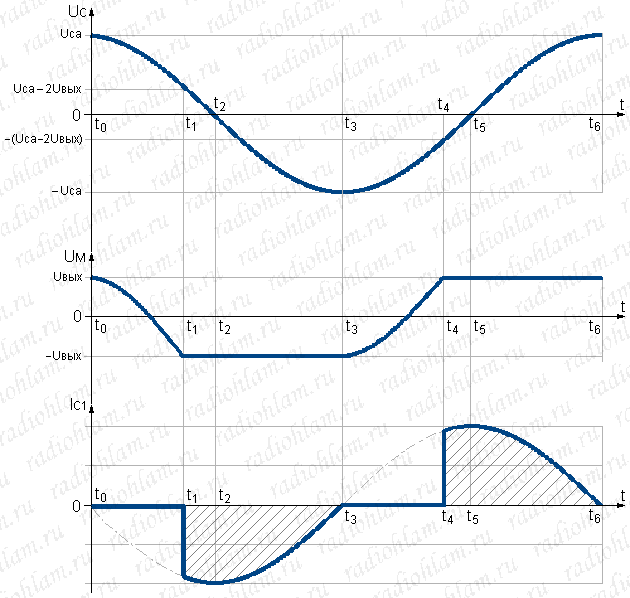
Рассуждаем следующим образом: в каждый момент времени полное напряжение и полный ток в этой цепи можно описать следующими уравнениями:
UC=UC1+UМ (1), iC=iC1+iМ (2)
В момент времени t0 уравнение напряжения примет вид: Uca=UC1+UМ. Поскольку Uca — это максимальное значение сетевого напряжения, то UC1 и UМ также в этот момент должны иметь максимальные значения (здесь в логике есть небольшой провал, максимум суммы — это не всегда сумма максимумов, функции могут быть сдвинуты по фазе, но… в общем, мы потом всё экспериментально проверим).
Максимальное значение UМ равно Uвых, поскольку если бы напряжение на мосту поднималось выше, то и конденсатор C2 заряжался бы до большего напряжения (мост бы открылся и к конденсатору C2 потёк бы зарядный ток, увеличивая напряжение на нём).
Токи через конденсатор и мост в момент t0 равны нулю. Про мост я выше уже написал (если бы через него тек ток, то конденсатор C2 заряжался бы дальше), а через C1 ток не течёт, поскольку ток через конденсатор — это первая производная от напряжения, которая в точках экстремума обращается в ноль (значит когда напряжение на конденсаторе максимально — ток равен нулю).
Далее сетевое напряжение (UC) начинает уменьшаться. При этом напряжение на C1 не меняется (тока-то через мост нет, заряд на C1 не меняется), следовательно вместе с падением UC уменьшается напряжение на входе моста.
В момент, когда сетевое напряжение упадёт до значения Uca-2Uвых (момент времени t1) — напряжение на входе моста достигнет значения -Uвых (находим с помощью формулы 1), диоды моста откроются и в первичной цепи (через мост и конденсатор C1) потечёт ток. При этом напряжение на входе моста перестанет меняться (помните, мы договорились, что ёмкость C2 достаточно большая для того, чтобы полностью сгладить пульсации).
Обратите внимание, что напряжение на входе моста в этот момент равно -Uм, так что ток потечёт в обратную сторону от того направления, в котором он тёк до момента времени t0. Этот ток, поскольку он течёт в обратную сторону, начнёт перезаряжать конденсатор C1.
К моменту времени t3 напряжение в сети достигнет максимума, только с противоположной относительно момента t0 полярностью. Соответственно, для этого момента экстремума сетевого напряжения будут справедливы все те же рассуждения касательно напряжений и токов, которые мы использовали для момента t0. То есть, к этому моменту конденсатор C1 полностью перезарядится (напряжение на нём достигнет максимального значения отрицательной полярности), а ток через C1 и мост упадёт до нуля.
Далее, по мере роста сетевого напряжения, напряжение на конденсаторе C1 будет оставаться неизменным, а напряжение на входе моста будет расти.
В момент времени t4, когда сетевое напряжение вырастет до значения -(Uca-2Uвых), напряжение на входе моста достигнет значения Uвых, диоды моста откроются и в первичной цепи (через мост и конденсатор C1) снова потечёт ток. Этот ток снова будет перезаряжать конденсатор C1, но уже напряжением положительной полярности.
В момент t6 напряжение на конденсаторе C1 достигнет максимального значения положительной полярности, а ток через C1 и мост упадёт до нуля.
Далее весь цикл повторится с самого начала.
Теперь давайте вспомним закон сохранения заряда. В соответствии с этим законом за один полный цикл через конденсатор C1, мост и нагрузку должно протекать одинаковое количество заряда. Поскольку ток нагрузки у нас постоянный, то количество заряда, протекающего через нагрузку за один цикл, можно найти по формуле Q=Iн*tцикла=Iн/fc, где fc — частота питающего сетевого напряжения. Количество заряда, протекающего через конденсатор C1, будет равно площади под графиком тока (заштрихованная площадь графика IC1(t)). Остаётся только найти эту площадь, приравнять её к заряду, протекающему за один цикл через нагрузку, и выразить из полученного выражения необходимую ёмкость конденсатора C1 в зависимости от тока нагрузки.
Подробные математические расчёты можно найти под вторым спойлером.
Итак, для заряда протекающего за один период через конденсатор С1 можно записать:
![]()
Косинусы найдём из графика сетевого напряжения, учитывая, что оно у нас на графике изменяется как раз по косинусоидальному закону, а так же учитывая его значения в моменты времени t1 и t3 (об этом мы говорили выше):
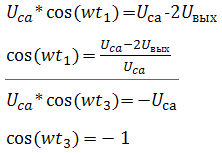
Максимальное значение тока через конденсатор C1 можно определить из формулы, связывающей ток, напряжение и реактивное сопротивление конденсатора:
![]()
Подставив всё это в выражение для заряда, получаем:
![]()
Используя полученное выражение и закон сохранения заряда находим ток через нагрузку:
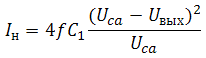
Если выходное напряжение много меньше сетевого питающего напряжения, то можно считать, что Uca-Uвых≈Uca. Тогда формулу можно переписать в упрощённом виде:
Iн=4fC1Uca
Можно наоборот, выразить ёмкость конденсатора C1 через ток нагрузки:
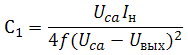
Упрощённый вариант формулы:
C1=Iн/(4fUca)
Итак, в результате расчётов мы получили следующие формулы:
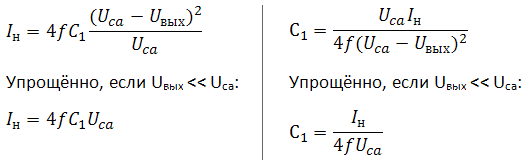
Обратите внимание, что в полученных формулах используется амплитудное значение сетевого напряжения, которое в корень из 2 раз больше действующего.
Кроме того, следует обратить внимание, что если ток нагрузки приравнять к нулю, то выходное напряжение схемы станет равно амплитуде сетевого напряжения (так что электролит скорее всего сразу пробьёт).
Ладно, самое главное мы посчитали, но это ещё не всё. Нужно учесть, что ток нагрузки и напряжение сети могут изменяться. Обеспечить работоспособность схемы во всём диапазоне питающих напряжений и рабочих токов — задача для стабилитрона. Рабочий диапазон токов нагрузки находится исходя из следующих соображений:
- При максимальном токе нагрузки и минимальном напряжении сети через стабилитрон должен протекать ток чуть больше минимального тока стабилизации (иначе выходное напряжение схемы будет меньше заданного)
- При минимальном токе нагрузки и максимальном питающем напряжении ток через стабилитрон должен быть чуть меньше максимального тока стабилизации (иначе стабилитрон попросту сгорит)
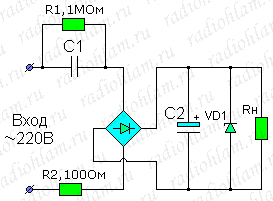
В окончательном, рабочем варианте добавим в схему пару резисторов:
- резистор с сопротивлением порядка 1 мегаома параллельно конденсатору C1 (через него конденсатор будет разряжаться при выключении схемы из сети)
- резистор с сопротивлением около сотни Ом, включенный последовательно с конденсатором и мостом (он будет работать как предохранитель и вместо него можно поставить обычный предохранитель)
Рабочий вариант схемы:
Online-калькулятор для расчёта блока питания с балластным конденсатором:
(для правильности расчётов используйте в качестве десятичной точки точку, а не запятую)
1) Исходные данные:
2) Расчётные данные:
Если в результате расчётов минимальный ток стабилитрона получился отрицательным — значит выбранная ёмкость конденсатора недостаточна для указанного тока нагрузки. Нужно либо увеличить ёмкость конденсатора, либо уменьшить максимальный ток нагрузки. Если же вы получили слишком большой максимальный ток стабилитрона, значит ёмкость наоборот слишком большая.